归并排序和快速排序

Posted on Edited on In Views:

一、归并排序(Merge sort)

  • 基本思路：借助额外空间，合并两个有序数组，得到更长的有序数组。

  • 算法思想：分而治之（分治思想）。

算法步骤：

归并排序算法是一个递归过程，边界条件为当输入序列仅有一个元素时，直接返回，具体过程如下：

1.如果输入内只有一个元素，则直接返回，否则将长度为 n 的输入序列分成两个长度为 n/2 的子序列；

2.分别对这两个子序列进行归并排序，使子序列变为有序状态；

3.设定两个指针，分别指向两个已经排序子序列的起始位置；

4.比较两个指针所指向的元素，选择相对小的元素放入到合并空间（用于存放排序结果），并移动指针到下一位置；

5.重复步骤 3 ~4 直到某一指针达到序列尾；

6.将另一序列剩下的所有元素直接复制到合并序列尾。

7.将合并空间排好序的数据复制到原数组的对应位置。

图解算法：

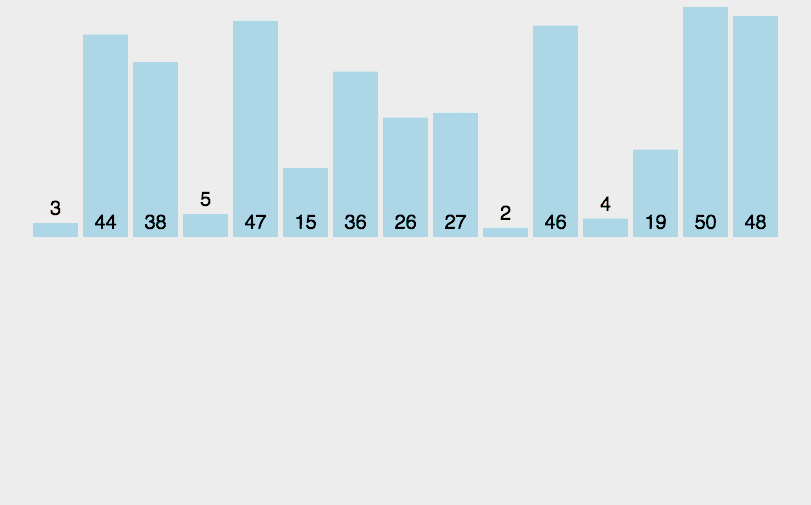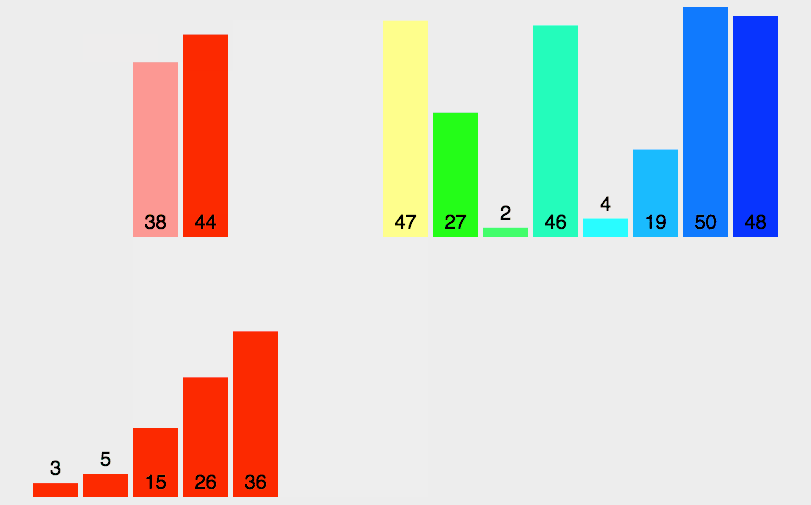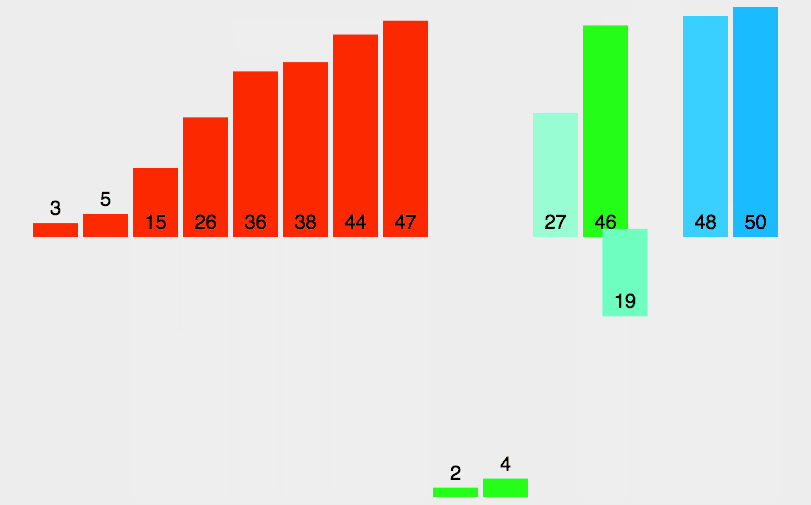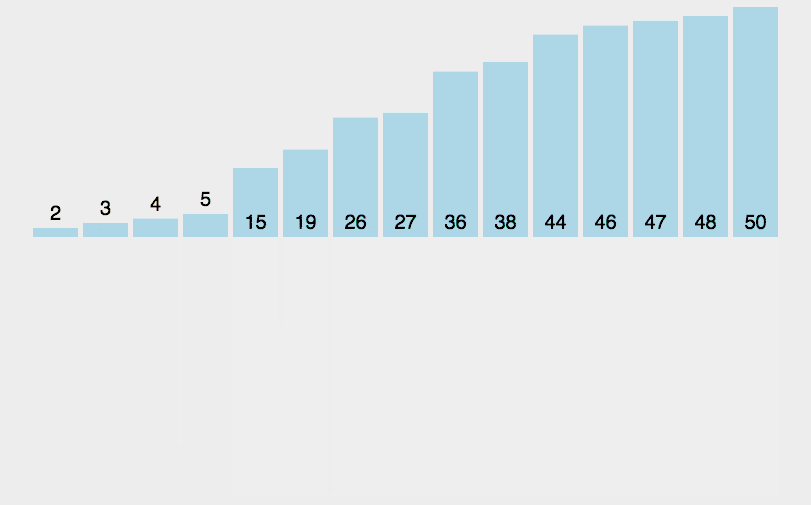
代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/* 归并排序 - 递归实现 */

/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/
void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
     int LeftEnd, NumElements, Tmp;
     int i;
     
     LeftEnd = R - 1; /* 左边终点位置 */
     Tmp = L;         /* 有序序列的起始位置 */
     NumElements = RightEnd - L + 1;
     
     while( L <= LeftEnd && R <= RightEnd ) {
         if ( A[L] <= A[R] )
             TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
         else
             TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
     }

     while( L <= LeftEnd )
         TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
     while( R <= RightEnd )
         TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
         
     for( i = 0; i < NumElements; i++, RightEnd -- )
         A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */
}

void Msort( ElementType A[], ElementType TmpA[], int L, int RightEnd )
{ /* 核心递归排序函数 */ 
     int Center;
     
     if ( L < RightEnd ) {
          Center = (L+RightEnd) / 2;
          Msort( A, TmpA, L, Center );              /* 递归解决左边 */ 
          Msort( A, TmpA, Center+1, RightEnd );     /* 递归解决右边 */  
          Merge( A, TmpA, L, Center+1, RightEnd );  /* 合并两段有序序列 */ 
     }
}

void MergeSort( ElementType A[], int N )
{ /* 归并排序 */
     ElementType *TmpA;
     TmpA = (ElementType *)malloc(N*sizeof(ElementType));
     
     if ( TmpA != NULL ) {
          Msort( A, TmpA, 0, N-1 );
          free( TmpA );
     }
     else printf( "空间不足" );
}
算法分析：
  • 稳定性：稳定
  • 时间复杂度 ：最佳：O(nlogn)， 最差：O(nlogn)， 平均：O(nlogn)
  • 空间复杂度 ：O(n)

二、快速排序(Quicksort)

算法步骤：

快速排序使用分治法(Divide and conquer)策略来把一个序列分为较小和较大的 2 个子序列，然后递回地排序两个子序列。具体算法描述如下：

1.从序列中随机挑出一个元素，做为"基准"(pivot)；

2.重新排列序列，将所有比基准值小的元素摆放在基准前面，所有比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个操作结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

3.递归地把小于基准值元素的子序列和大于基准值元素的子序列进行快速排序。

实现细节：

1.怎么选取pivot：

  • 调用随件函数，获得随机的pivot
  • 取数组头，中，尾三个数的中位数作为pivot

2.子集划分过程：

  • 每趟排序后，将与分界元素相等的元素聚集在分界元素周围，这样可以避免极端数据（如序列中大部分元素都相等）带来的退化。

3.当序列较短时，使用插入排序的效率更高。

图解算法:

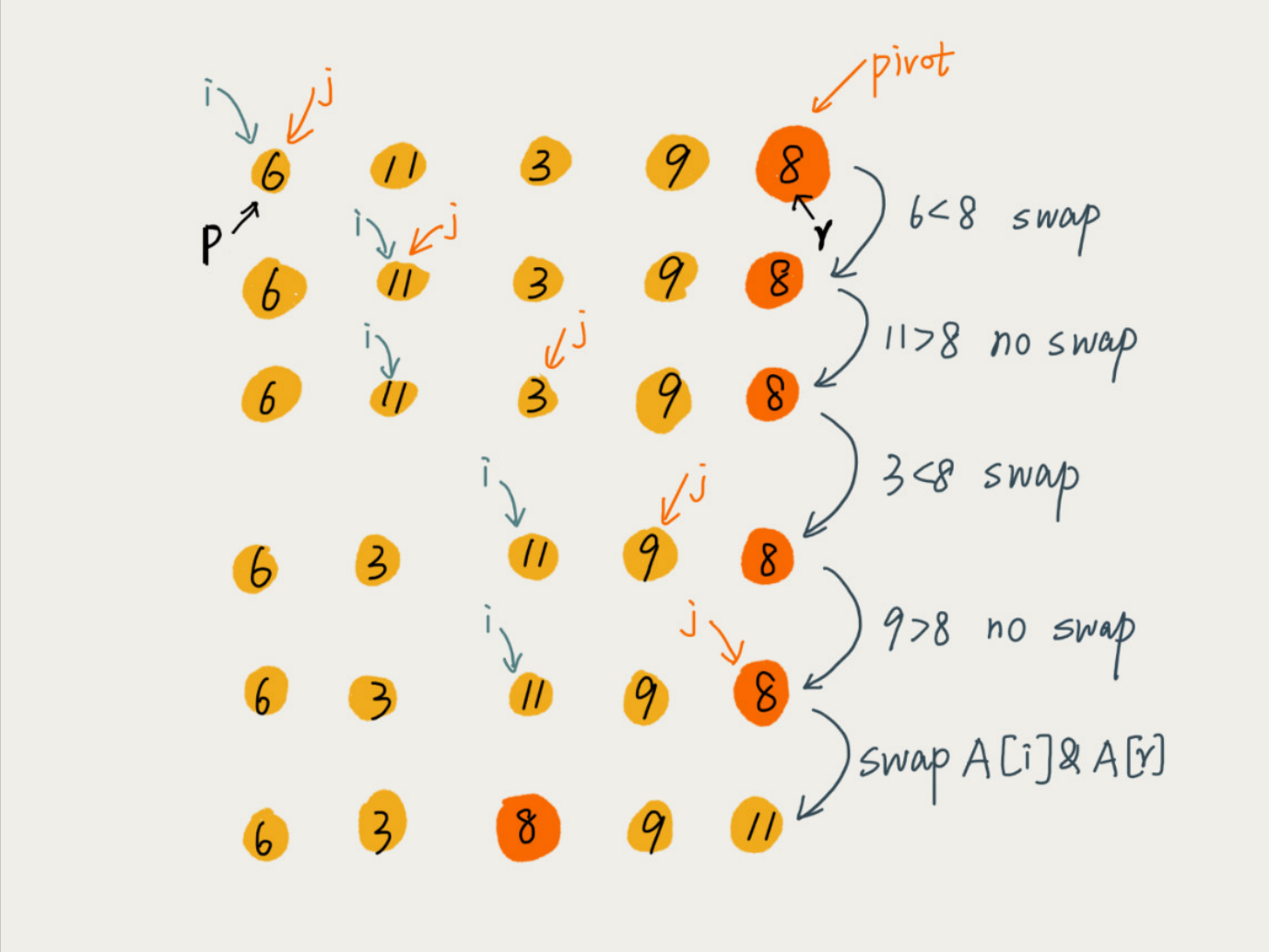
代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public class QuickSort {

  // 快速排序，a是数组，n表示数组的大小
  public static void quickSort(int[] a, int n) {
    quickSortInternally(a, 0, n-1);
  }

  // 快速排序递归函数，p,r为下标
  private static void quickSortInternally(int[] a, int p, int r) {
    if (p >= r) return;

    int q = partition(a, p, r); // 获取分区点
    quickSortInternally(a, p, q-1);
    quickSortInternally(a, q+1, r);
  }

  private static int partition(int[] a, int p, int r) {
    int pivot = a[r];
    int i = p;
    for(int j = p; j < r; ++j) {
      if (a[j] < pivot) {
        if (i == j) {
          ++i;
        } else {
          int tmp = a[i];
          a[i] = a[j];
          a[j] = tmp;
          ++i;
        }
      }
    }

    int tmp = a[i];
    a[i] = a[r];
    a[r] = tmp;

    System.out.println("i=" + i);
    return i;
  }
}

三、两者的区别

归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。我们前面讲过，归并之所以是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。